Slices of Topology
No matter how you slice it and dice it, you get out the same information. Well, that's not exactly true. But I'll show you one way you can look at individual slices of a shape in order to determine its overall topology.
Set Up
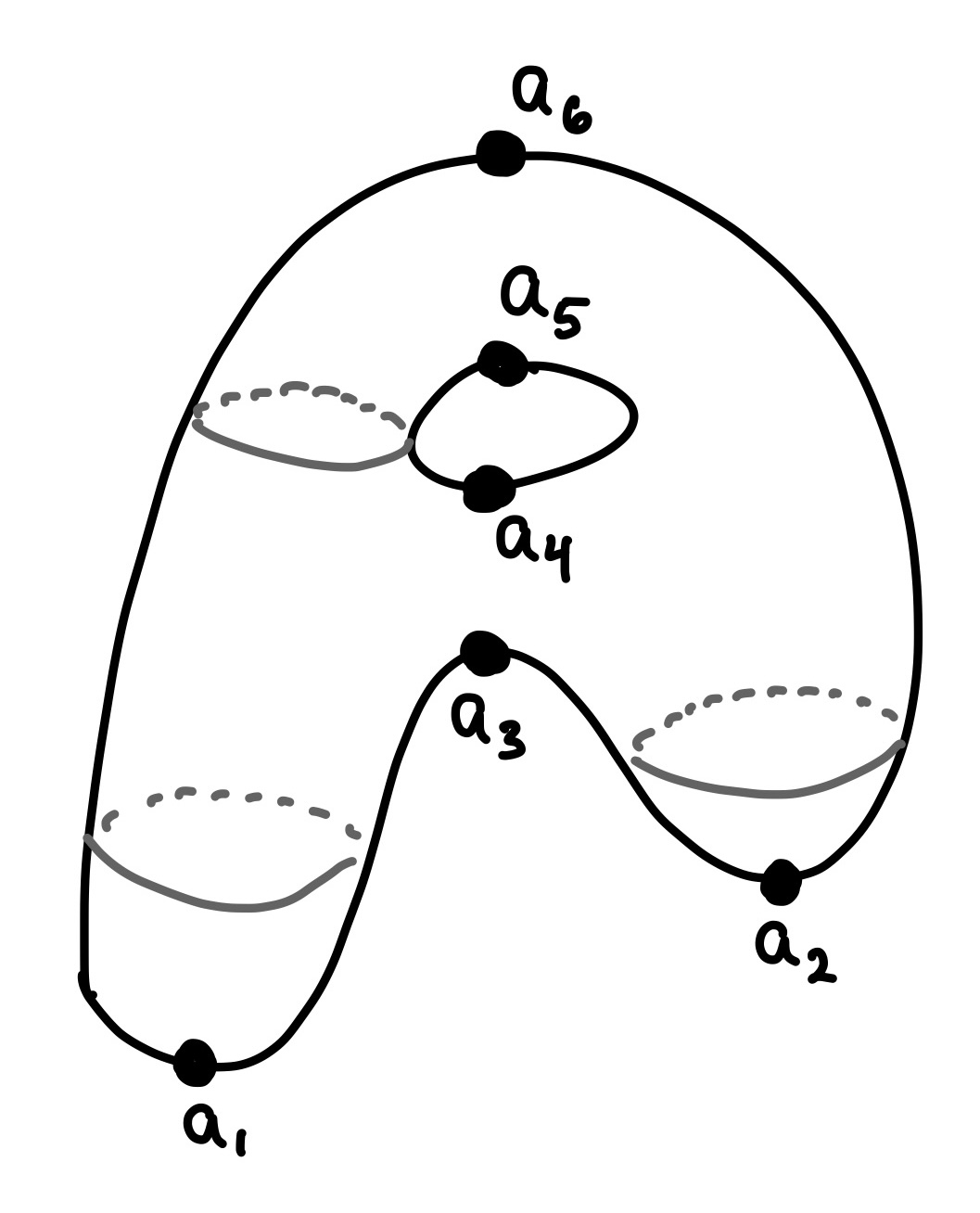
This is basically a hollow donut with legs. Said differently, it's a shell of a sphere with a hole in it (so it's like a torus), with the lower bits stretched out. This three-dimensional shape has six total local minima and local maxima, which are called critical values. They are labelled as \(a_1\) through \(a_6\).
We are going to look at one particular strategy we can use to slice this shape into smaller pieces. We'll then look at each piece individually and determine what shape it is. For example, each piece could be a point or a circle or a sphere or something else. We'll also take note of how many consecutive slices contain each particular shape.
Slicing: Levelsets Zigzag Persistent Homology
This slicing strategy considers each horizontal slides through each critical value ( \(a_1\) through \(a_6\) ) and each horizontal region between adjacent critical values.
We are going to keep track of three different types of shapes: connected components ( \(H_0\) ), loops ( \(H_1\) ), and voids ( \(H_2\) ).

- \(a_1\). A single point.
- \(H_0\): Something exists; thus our first connected component is born.
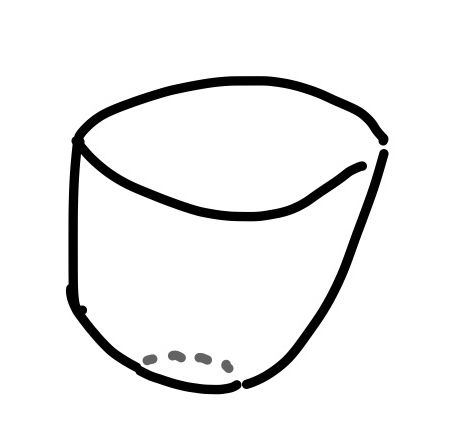
- \((a_1, a_2)\). A cylinder that's missing its top and bottom.
- \(H_0\): Something still exists, so our connected component is still alive.
- \(H_1\): Also, a loop is born; this is the loop you can create by drawing a circle around the outside of the cylinder.
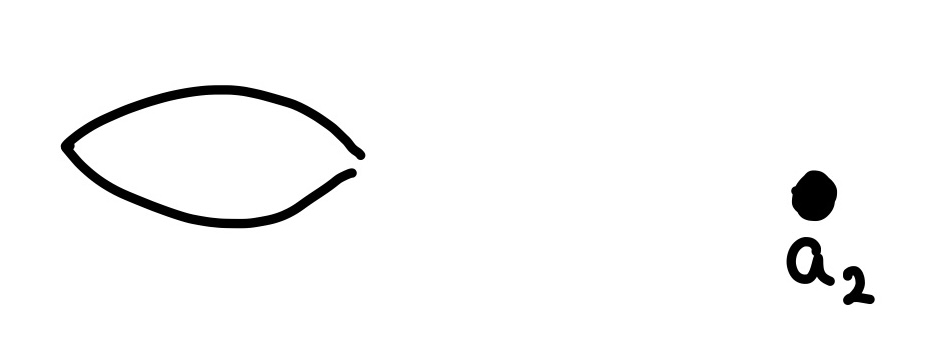
- \(a_2\). A single point and a loop.
- \(H_0\): The original connected component still exists. Also, a second thing exists; thus our second connected component is born.
- \(H_1\): The loop is still alive.
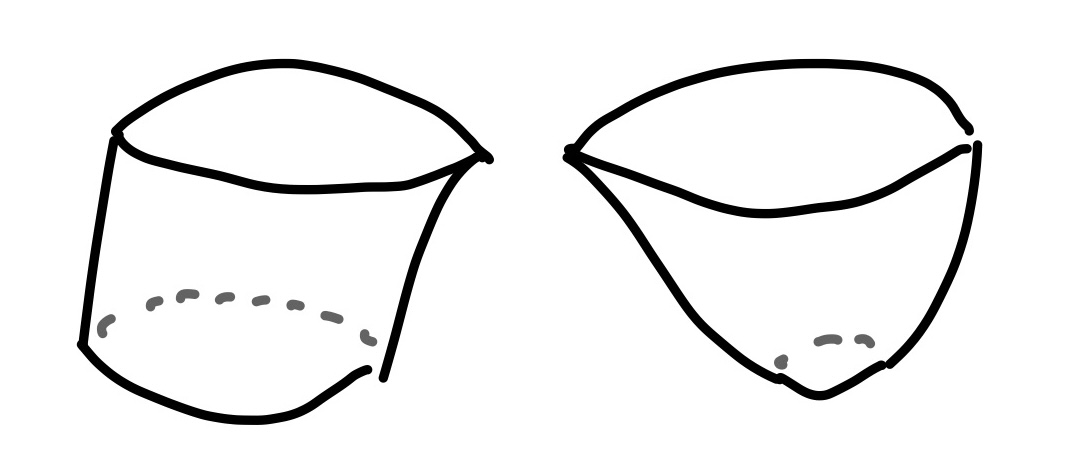
- \((a_2, a_3)\). Two separate cylinders.
- \(H_0\): Two connected components.
- \(H_1\): The previous loop still exists, and a second loop is born.
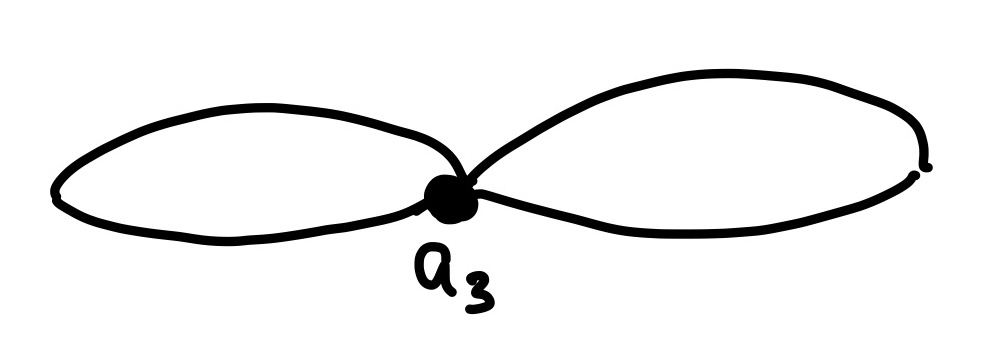
- \(a_3\). Two loops connected at a point.
- \(H_0\): Only one connected component remains.
- \(H_1\): Both loops still exist.
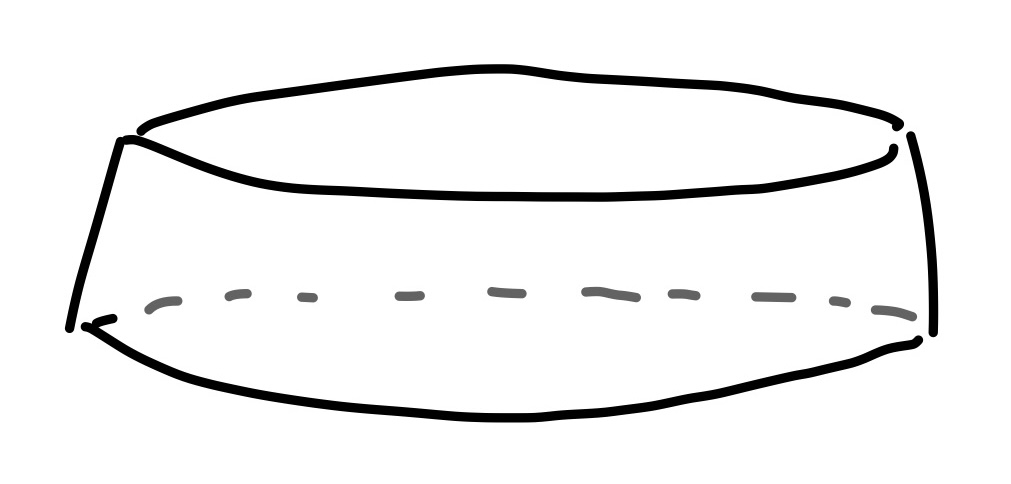
- \((a_3, a_4)\). A single cylinder.
- \(H_0\): A single connected component.
- \(H_1\): Only one loop remains.
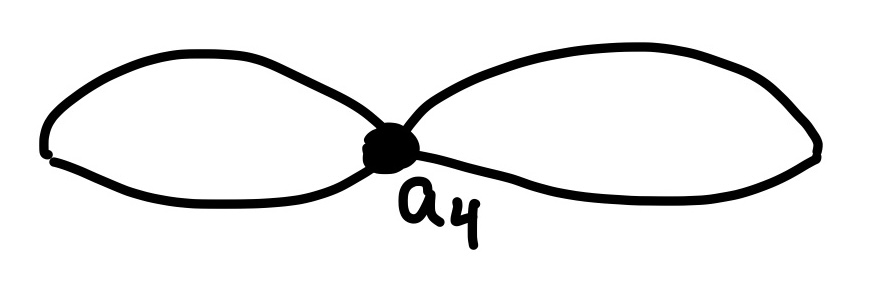
- \(a_4\). Two loops connected at a point.
- \(H_0\): Still have a single connected component.
- \(H_1\): A second loop is alive again.
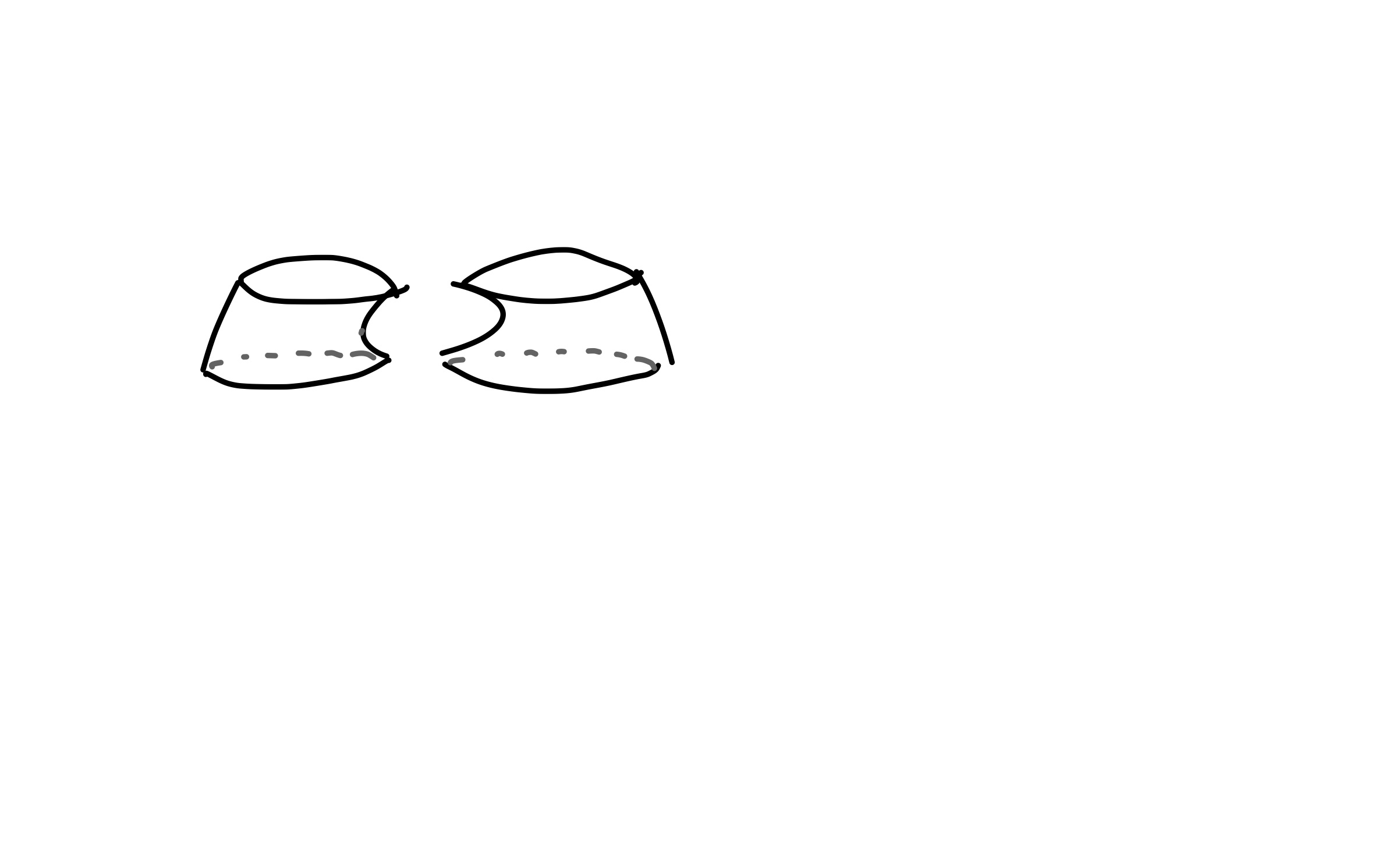
- \((a_4, a_5)\). Two separate cylinders.
- \(H_0\): A second connected component is alive again.
- \(H_1\): A second loop is alive again.
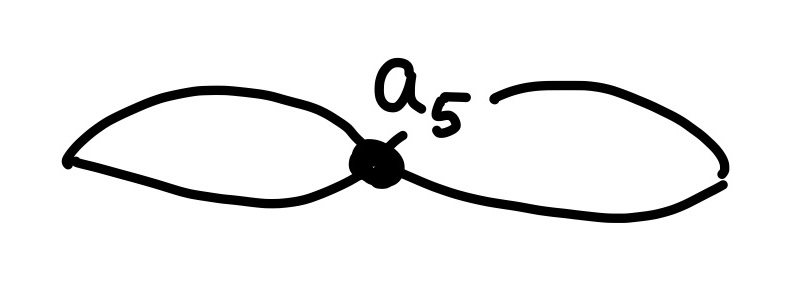
- \(a_5\). Two loops connected at a point.
- \(H_0\): Only one connected component remains.
- \(H_1\): Still have both loops.
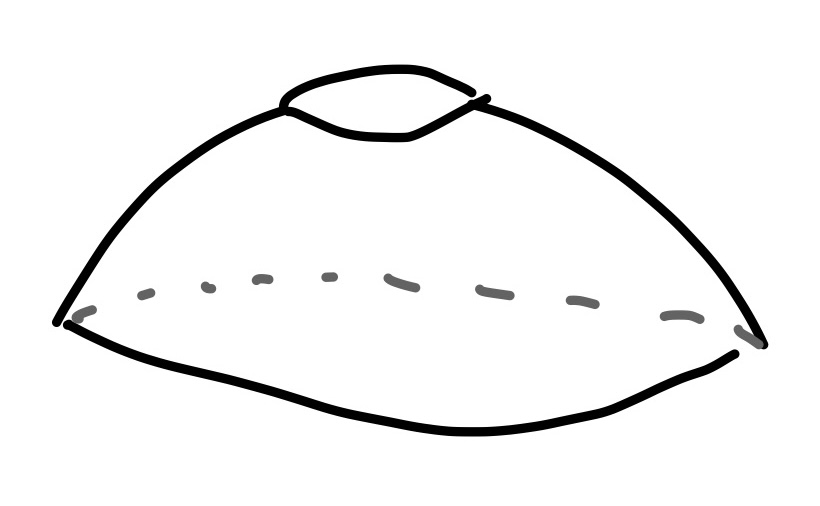
- \((a_5, a_6)\). A single cylinder.
- \(H_0\): Still have a single connected component.
- \(H_1\): Only one loop remains.

- \(a_6\). A single point.
- \(H_0\): A single connected component remains.
- \(H_1\): There are no loops.
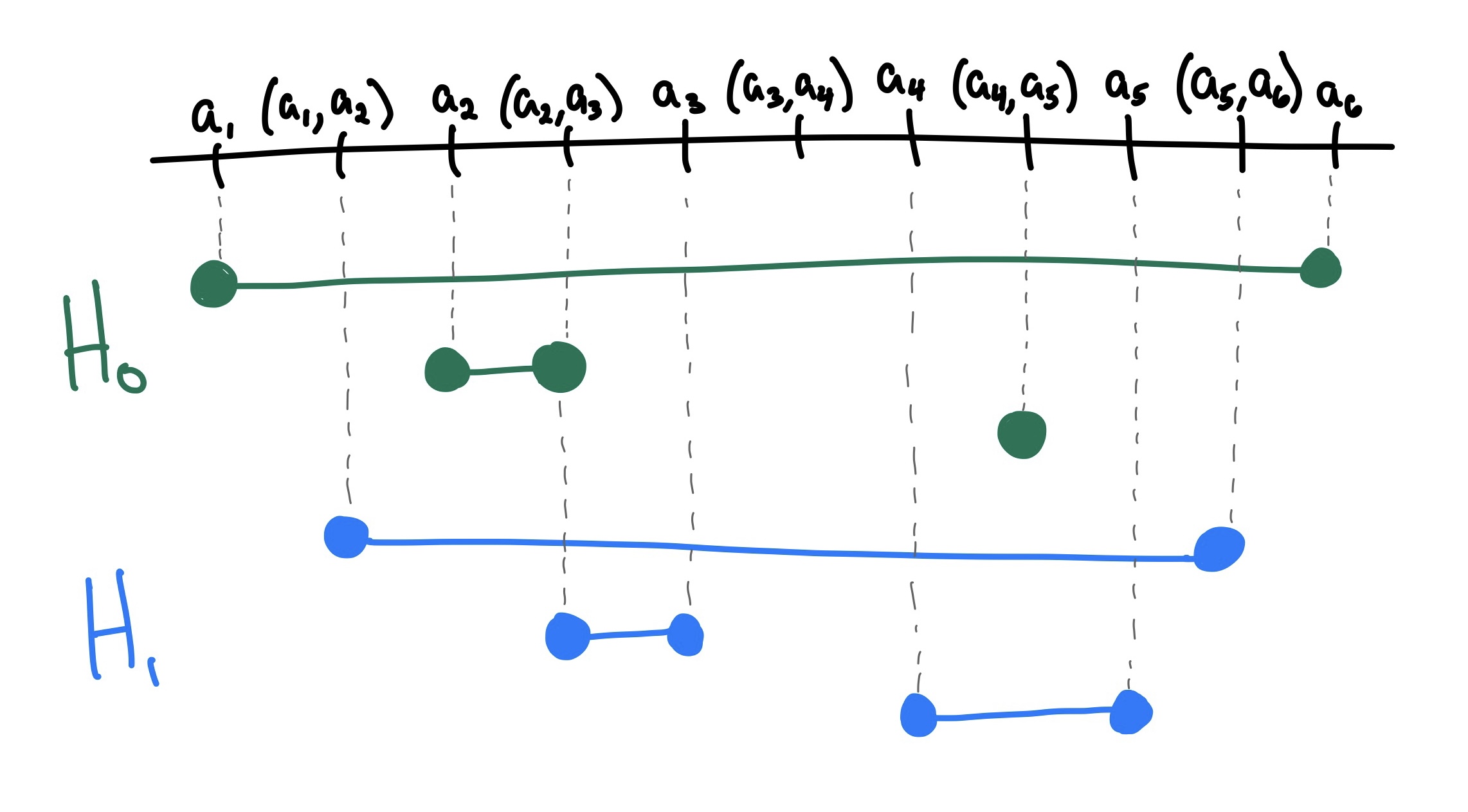
We can represent all of that information in a single barcode diagram. Given the barcode diagram, how different an original shape could you draw?
Talk Slides
I gave a talk about this topic at the weekly University of Florida research group meeting for Topological Data Analysis (TDA).
Here is a pdf of the slides I used for the talk.